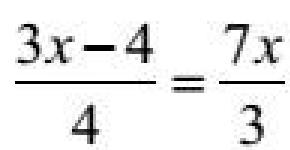Riešte rovnice pre 5. ročník. Riešenie lineárnych rovníc s príkladmi

Rovnica s jednou neznámou, ktorá po otvorení zátvoriek a prinesení podobných pojmov nadobudne tvar

ax + b = 0, kde a a b sú ľubovoľné čísla, sa nazýva lineárna rovnica s jednou neznámou. Dnes zistíme, ako vyriešiť tieto lineárne rovnice.

Napríklad všetky rovnice:

2x + 3= 7 – 0,5x; 0,3x = 0; x/2 + 3 = 1/2 (x – 2) - lineárne.

Hodnota neznámej, ktorá mení rovnicu na skutočnú rovnosť, sa nazýva rozhodnutie alebo koreň rovnice .

Napríklad, ak do rovnice 3x + 7 = 13 namiesto neznámeho x dosadíme číslo 2, dostaneme správnu rovnosť 3 2 +7 = 13. To znamená, že hodnota x = 2 je riešením alebo koreňom rovnice.

A hodnota x = 3 nezmení rovnicu 3x + 7 = 13 na skutočnú rovnosť, pretože 3 2 +7 ≠ 13. To znamená, že hodnota x = 3 nie je riešením ani koreňom rovnice.

Riešenie akýchkoľvek lineárnych rovníc sa redukuje na riešenie rovníc vo forme

ax + b = 0.

Presuňme voľný člen z ľavej strany rovnice doprava, pričom znamienko pred b zmeníme na opačné, dostaneme

Ak a ≠ 0, potom x = ‒ b/a .

Príklad 1 Riešte rovnicu 3x + 2 =11.

Presuňme 2 z ľavej strany rovnice doprava, pričom znamienko pred 2 zmeníme na opačné, dostaneme
3x = 11 – 2.

Tak urobme odčítanie
3x = 9.

Ak chcete nájsť x, musíte rozdeliť produkt známym faktorom, tj
x = 9:3.

To znamená, že hodnota x = 3 je riešením alebo koreňom rovnice.

Odpoveď: x = 3.

Ak a = 0 a b = 0, potom dostaneme rovnicu 0x = 0. Táto rovnica má nekonečne veľa riešení, keďže keď vynásobíme ľubovoľné číslo 0, dostaneme 0, ale b sa tiež rovná 0. Riešením tejto rovnice je ľubovoľné číslo.

Príklad 2 Vyriešte rovnicu 5(x – 3) + 2 = 3 (x – 4) + 2x ‒ 1.

Rozšírime zátvorky:
5x – 15 + 2 = 3x – 12 + 2x ‒ 1.

5x – 3x ‒ 2x = – 12 ‒ 1 + 15 ‒ 2.

Tu je niekoľko podobných výrazov:
0x = 0.

Odpoveď: x - ľubovoľné číslo.

Ak a = 0 a b ≠ 0, potom dostaneme rovnicu 0х = - b. Táto rovnica nemá riešenia, pretože keď vynásobíme ľubovoľné číslo 0, dostaneme 0, ale b ≠ 0.

Príklad 3 Vyriešte rovnicu x + 8 = x + 5.

Zoskupme výrazy obsahujúce neznáme na ľavej strane a voľné výrazy na pravej strane:
x – x = 5 – 8.

Tu je niekoľko podobných výrazov:
0х = ‒ 3.

Odpoveď: žiadne riešenia.

Zapnuté postava 1 ukazuje schému riešenia lineárnej rovnice

Zostavme si všeobecnú schému riešenia rovníc s jednou premennou. Pozrime sa na riešenie príkladu 4.

Príklad 4. Predpokladajme, že potrebujeme vyriešiť rovnicu

1) Vynásobte všetky členy rovnice najmenším spoločným násobkom menovateľov, ktorý sa rovná 12.

2) Po zmenšení dostaneme
4 (x – 4) + 3 2 (x + 1) ‒ 12 = 6 5 (x – 3) + 24x – 2 (11x + 43)

3) Ak chcete oddeliť výrazy obsahujúce neznáme a voľné výrazy, otvorte zátvorky:
4x – 16 + 6x + 6 – 12 = 30x – 90 + 24x – 22x – 86.

4) Zoskupme do jednej časti výrazy obsahujúce neznáme a do druhej voľné výrazy:
4x + 6x – 30x – 24x + 22x = ‒ 90 – 86 + 16 – 6 + 12.

5) Uveďme podobné pojmy:
- 22 x = - 154.

6) Vydelíme – 22, dostaneme
x = 7.

Ako vidíte, koreň rovnice je sedem.

Vo všeobecnosti takéto rovnice je možné riešiť pomocou nasledujúcej schémy:

a) priviesť rovnicu do jej celočíselného tvaru;

b) otvorte zátvorky;

c) zoskupiť členy obsahujúce neznámu v jednej časti rovnice a voľné členy v druhej;

d) priviesť podobných členov;

e) vyriešte rovnicu tvaru aх = b, ktorá bola získaná po prinesení podobných členov.

Táto schéma však nie je potrebná pre každú rovnicu. Pri riešení mnohých jednoduchších rovníc musíte začať nie od prvej, ale od druhej ( Príklad. 2), tretí ( Príklad. 13) a dokonca aj od piatej fázy, ako v príklade 5.

Príklad 5. Riešte rovnicu 2x = 1/4.

Nájdite neznámu x = 1/4: 2,
x = 1/8 .

Pozrime sa na riešenie niektorých lineárnych rovníc nájdených v hlavnej štátnej skúške.

Príklad 6. Riešte rovnicu 2 (x + 3) = 5 – 6x.

2x + 6 = 5 – 6x

2x + 6x = 5 – 6

Odpoveď: - 0,125

Príklad 7. Vyriešte rovnicu – 6 (5 – 3x) = 8x – 7.

– 30 + 18x = 8x – 7

18x – 8x = – 7 +30

Odpoveď: 2.3

Príklad 8. Vyriešte rovnicu

3(3x – 4) = 4 7x + 24

9x – 12 = 28x + 24

9x – 28x = 24 + 12

Príklad 9. Nájdite f(6), ak f (x + 2) = 3 7

Riešenie

Keďže potrebujeme nájsť f(6) a vieme f (x + 2),
potom x + 2 = 6.

Riešime lineárnu rovnicu x + 2 = 6,
dostaneme x = 6 – 2, x = 4.

Ak x = 4, potom
f(6) = 3 7-4 = 3 3 = 27

odpoveď: 27.

Ak máte ešte otázky alebo chcete riešeniu rovníc porozumieť dôkladnejšie, prihláste sa na moje hodiny v ROZVRHU. Rád vám pomôžem!

TutorOnline tiež odporúča pozrieť si novú video lekciu od našej lektorky Olgy Alexandrovny, ktorá vám pomôže pochopiť lineárne rovnice aj iné.

webová stránka, pri kopírovaní celého materiálu alebo jeho časti je potrebný odkaz na zdroj.

Jedna z najdôležitejších zručností, keď prijatie do 5. ročníka je schopnosť riešiť jednoduché rovnice. Keďže 5. ročník ešte nie je tak ďaleko od základnej školy, nie je toľko druhov rovníc, ktoré žiak dokáže vyriešiť. Predstavíme vám všetky základné typy rovníc, ktoré ak chcete, musíte vedieť riešiť vstúpiť na fyzikálnu a matematickú školu.

Typ 1: "cibuľovitý"
Toto sú rovnice, s ktorými sa takmer pravdepodobne stretnete prijatie na akúkoľvek školu alebo krúžok 5. ročníka ako samostatná úloha. Je ľahké ich odlíšiť od ostatných: premenná je v nich prítomná iba raz. Napríklad, alebo.
Sú vyriešené veľmi jednoducho: stačí sa „dostať“ do neznáma, postupne „odstraňovať“ všetko nepotrebné, čo ho obklopuje – ako keby ste šúpali cibuľu – odtiaľ názov. Aby ste to vyriešili, stačí si spomenúť na niekoľko pravidiel z druhej triedy. Poďme si ich všetky vymenovať:

Doplnenie

termín1 + termín2 = súčet
termín1 = súčet - termín2
termín2 = súčet - termín1

Odčítanie

minuend - subtrahend = rozdiel
minuend = subtrahend + rozdiel
subtrahend = minuend - rozdiel

Násobenie

faktor 1 * faktor 2 = produkt
faktor1 = produkt: faktor2
faktor2 = produkt: faktor1

divízie

dividenda: deliteľ = podiel
dividenda = deliteľ * kvocient
deliteľ = dividenda: kvocient

Pozrime sa na príklad, ako tieto pravidlá aplikovať.

Všimnite si, že sa delíme na a dostávame . V tejto situácii poznáme deliteľa a kvocientu. Ak chcete nájsť dividendu, musíte vynásobiť deliteľa podielom:

Stali sme sa o niečo bližšie k sebe. Teraz to vidíme sa pridá a ukáže sa . To znamená, že ak chcete nájsť jeden z výrazov, musíte od súčtu odčítať známy výraz:

A ďalšia „vrstva“ bola odstránená z neznáma! Teraz vidíme situáciu so známou hodnotou produktu () a jedným známym faktorom ().

Teraz je situácia „minuend - subtrahend = rozdiel“

A posledným krokom je známy produkt () a jeden z faktorov ()

Typ 2: rovnice so zátvorkami
Rovnice tohto typu sa najčastejšie nachádzajú v úlohách - 90% všetkých úloh pre prijatie do 5. ročníka. Na rozdiel od "cibuľové rovnice" premenná sa tu môže objaviť viackrát, takže nie je možné ju vyriešiť metódami z predchádzajúceho odseku. Typické rovnice: alebo
Hlavným problémom je správne otváranie držiakov. Keď sa vám to podarí urobiť správne, mali by ste zredukovať podobné výrazy (čísla na čísla, premenné na premenné) a potom dostaneme najjednoduchšie "cibuľová rovnica" ktoré vieme vyriešiť. Ale najprv to.

Rozširujúce zátvorky. Dáme niekoľko pravidiel, ktoré by sa mali v tomto prípade použiť. Ako však ukazuje prax, študent začne správne otvárať zátvorky až po 70 - 80 dokončených problémoch. Základné pravidlo je toto: akýkoľvek faktor mimo zátvoriek sa musí vynásobiť každým výrazom v zátvorkách. A znamienko mínus pred zátvorkou zmení znamienko všetkých výrazov vo vnútri. Takže základné pravidlá zverejňovania:

Prinášať podobné. Tu je všetko oveľa jednoduchšie: prenosom výrazov cez znamienko rovnosti musíte zabezpečiť, aby na jednej strane boli iba pojmy s neznámym a na druhej strane iba čísla. Základné pravidlo je toto: každý prenesený výraz zmení svoje znamienko – ak bol s, stane sa s a naopak. Po úspešnom prenose je potrebné spočítať celkový počet neznámych, celkový počet na druhej strane rovnosti ako premenné a vyriešiť jednoduchý "cibuľová rovnica".

Rovnica je rovnosť, v ktorej je neznámy člen – x. Jeho zmysel treba nájsť.

Neznáma veličina sa nazýva koreň rovnice. Riešenie rovnice znamená nájsť jej koreň a na to potrebujete poznať vlastnosti rovníc. Rovnice pre ročník 5 nie sú ťažké, ale ak sa ich naučíte správne riešiť, nebudete s nimi mať v budúcnosti problémy.

Hlavná vlastnosť rovníc

Keď sa obe strany rovnice zmenia o rovnakú hodnotu, zostáva to tá istá rovnica s rovnakým koreňom. Poďme vyriešiť niekoľko príkladov, aby sme lepšie pochopili toto pravidlo.

Ako riešiť rovnice: sčítanie alebo odčítanie

Predpokladajme, že máme rovnicu v tvare:

a + x = b - tu a a b sú čísla a x je neznámy člen rovnice.

Ak pripočítame (alebo od nich odčítame) hodnotu c na obe strany rovnice, nezmení sa:

a + x + c = b + c
a + x - c = b - c.

Príklad 1

Využime túto vlastnosť na vyriešenie rovnice:

37+x=51

Odčítajte číslo 37 z oboch strán:

37+x-37=51-37

dostaneme:

x = 51-37.

Koreň rovnice je x=14.

Ak sa pozorne pozrieme na poslednú rovnicu, vidíme, že je rovnaká ako prvá. Jednoducho sme presunuli člen 37 z jednej strany rovnice na druhú a nahradili sme plus mínusom.

Ukazuje sa, že ľubovoľné číslo možno preniesť z jednej časti rovnice do druhej s opačným znamienkom.

Príklad 2

37+x=37+22

Urobme rovnakú akciu, presuňte číslo 37 z ľavej strany rovnice doprava:

x=37-37+22

Keďže 37-37=0, jednoducho to znížime a dostaneme:

x = 22.

Identické členy rovnice s rovnakým znamienkom, ktoré sa nachádzajú v rôznych častiach rovnice, možno zmenšiť (prečiarknuť).

Násobenie a delenie rovníc

Obidve strany rovnosti možno tiež vynásobiť alebo vydeliť rovnakým číslom:

Ak sa rovnosť a = b vydelí alebo vynásobí c, nemení sa:

a/c = b/c,
ac = bс.

Príklad 3

5x = 20

Vydeľme obe strany rovnice 5:

5x/5 = 20/5.

Pretože 5/5 = 1, znížime tieto násobiteľa a deliteľa na ľavej strane rovnice a dostaneme:

x = 20/5, x = 4

Príklad 4

5x = 5a

Ak sú obe strany rovnice delené 5, dostaneme:

5x/5 = 5a/5.

Číslo 5 v čitateli a menovateli ľavej a pravej strany sa ruší, výsledkom čoho je x = a. To znamená, že rovnaké faktory na ľavej a pravej strane rovníc sa rušia.

Vyriešime ďalší príklad:

13 + 2x = 21

Posúvame člen 13 z ľavej strany rovnice doprava s opačným znamienkom:

2x = 21 - 13
2x = 8.

Vydelením oboch strán rovnice 2 dostaneme:

x = 4.

Lekcia č. 33

Téma: Rovnice

Ciele lekcie:

Zhrňte a systematizujte vedomosti študentov o študovanej téme, pokračujte v práci na rozvíjaní schopnosti riešiť rovnice a problémy skladaním rovníc.

Zlepšiť počítačové zručnosti študentov

Podporujte zodpovedný prístup k učeniu.

Kritériá úspešnosti

Viem …

Rozumiem …

Môžem ….

Počas vyučovania

Úvodný – motivačný moment

Matematika, priatelia,
Potrebuje to úplne každý.
V triede pracujte usilovne
A úspech vás určite čaká!

Dnes pokračujeme v učení sa, ako riešiť rovnice a úlohy pomocou metódy rovníc.

Aktualizácia vedomostí

Na splnenie úloh si zopakujeme základné pojmy potrebné na riešenie rovníc a problémov, ktoré sa riešia skladaním rovníc.

( )

Aký druh rovnosti sa nazýva rovnica?

Aké číslo sa nazýva koreň rovnice?

Čo znamená vyriešiť rovnicu?

Ako skontrolovať, či je rovnica vyriešená správne?

Kontrola dokončenia domácej úlohy (Snímka č. 2)

(kontrola dokončenia domácej úlohy sa vykonáva pomocou autotestu)

Riešenie študentmi s výslovnosťou

(x – 87) – 27 = 36

87 – (41 + y) = 22

x – 87 = 36 + 27

41 + y = 87 - 22

x – 87 = 63

41 + y = 65

x = 63 + 87

y = 65 - 41

x = 150

y = 24

Vyšetrenie

(150 – 87) - = 36

87 – (41 + 24) = 22

63 – 27 = 36

87 – 65 = 22

36 = 36 (správne)

22 = 22 (správne)

Ústna práca

1.Pomenujte čísla rovníc (rovnice sú napísané na tabuli), v ktorých treba daný výraz nájsť.
V ktorých rovniciach je minuend neznámy?
V ktorých rovniciach potrebujete nájsť podtrahend?
V ktorých rovniciach je pojem neznámy?
Nájdite korene rovníc.

x + 21 = 40; 2) a – 21 = 40; 3) 50 = a + 31; 4) s – 23 = 61; 5) 42 = 70 – y;

6) 38 - x = 38; 7) 25 – a = 25; 8) x + 32 = 32; 9) y – 0 = 27; 10) 60 – s = 35

(Snímka č. 3)

Skupinová práca
Nájdite neznáme číslo:

1) K neznámym sme pridali 71 a dostali sme 100.
(x + 71 = 100)
x = 100 – 71
x = 29
2) Súčin dvoch čísel je 72, jeden faktor je 12, nájdite druhý faktor.
12*X = 72
X = 72:12
X = 6
3) Pri delení určitého čísla číslom 9 je podiel 11. Nájdite toto číslo.
x: 9 = 31
x = 31* 9
x = 279

Práca s rovnicami (Snímka č. 5)

Študenti sú požiadaní, aby vytvorili tri rovnice podľa podmienok a vyriešili tieto rovnice v nasledujúcom poradí:
1) Rozdiel medzi súčtom čísel „x“ a 40 je väčší ako číslo 31 x 50.
(Rovnica je vyriešená s komentárom)
2) Číslo 70 je väčšie ako súčet čísla 25 a „y“ o 38.
(Žiaci riešia rovnicu samostatne a jeden zo študentov napíše riešenie na zadnú stranu tabule)
3) Rozdiel medzi číslom 120 a číslom „a“ je menší ako číslo 65 o 53.
(Riešenie rovnice sa celé zapíše na tabuľu, potom celá trieda diskutuje o riešení rovnice)

Práca na úlohách (snímka číslo 6)

Úloha č.1
V krabici bolo niekoľko jabĺk. Po vložení ďalších 32 jabĺk ich bolo 81. Koľko jabĺk bolo pôvodne v krabici?

Čo hovorí problém? Aké akcie ste vykonali s jablkami? Čo potrebujete vedieť v probléme? Čo by malo písmeno predstavovať?
Nech je v košíku x jabĺk. Po vložení ďalších 32 jabĺk bolo (x + 32) jabĺk a podľa podmienok problému bolo v košíku 81 jabĺk.
Môžeme teda vytvoriť rovnicu:
x + 32 = 81,
x = 81 – 32,
x = 49

Pôvodne bolo v košíku 49 jabĺk.
Odpoveď: 49 jabĺk.

Problém č.2
Ateliér mal 70 (m) látky. Z časti látky boli ušité šaty a ďalších 18 (m) bolo použitých na nohavice, po ktorých zostalo 23 (m). Koľko metrov látky bolo použitých na šaty?

Čo hovorí problém? Aké akcie ste vykonali s látkou? Čo potrebujete vedieť v probléme? Čo by malo písmeno predstavovať?
Na šaty nech sa použije x (m) látky. Potom sa (x + 18) metrov látky spotrebovalo na ušitie šiat a nohavíc. Podľa podmienok problému je známe, že zostáva 23 m.
Môžeme teda vytvoriť rovnicu:
70 – (x + 18) = 23,
x + 18 = 70 – 23,
x + 18 = 47,
x = 47 – 18,
x = 29.

Na šaty bolo použitých 29 metrov látky.
Odpoveď: 29 metrov.

Samostatná práca (Snímka č. 7)

Samostatná práca je študentom ponúkaná v dvoch variantoch.

1 možnosť

Možnosť 2

Riešte rovnice:

1) 320 – x = 176

1) 450 – y = 246

2) y + 294 = 501

2) x + 386 = 602